La hipérbola es el lugar geométrico de los puntos del plano cuya diferencia de distancias a los puntos fijos llamados focos es constante.
ELEMENTOS DE LA HIPÉRBOLA
Focos: Son los puntos fijos F y F'.
Eje focal: Es la recta que pasa por los focos.
Centro: Es el punto de intersección de los ejes.
Vértices: Los puntos A y A' son los puntos de intersección de la hipérbola con el eje focal.
Los puntos B y B' se obtienen como intersección del eje imaginario con la circunferencia que tiene por centro uno de los vértices y de radio c.
Distancia focal: Es el segmento  de longitud 2c.
de longitud 2c.
 de longitud 2c.
de longitud 2c.Eje mayor: Es el segmento  de longitud 2a.
de longitud 2a.
 de longitud 2a.
de longitud 2a.Eje menor: Es el segmento  de longitud 2b.
de longitud 2b.
 de longitud 2b.
de longitud 2b.Ejes de simetría: Son las rectas que contienen al eje real o al eje imaginario.
(puntos relacionados con la imagen anterior).
TIPOS Y CARACTERÍSTICAS
Características
1. La hipérbola posee una excentricidad mayor que uno, la cual se define como la distancia del centro hacia
uno de los focos, dividida, la distancia del centro a uno de los vértices.
2. La longitud del eje mayor se define como dos veces la distancia del centro hacia cualquiera de los puntos del eje mayor.
3. La longitud del eje conjugado se define como dos veces la distancia del centro hacia cualquiera de los
puntos del vértice del eje menor.
1. La hipérbola posee una excentricidad mayor que uno, la cual se define como la distancia del centro hacia
uno de los focos, dividida, la distancia del centro a uno de los vértices.
2. La longitud del eje mayor se define como dos veces la distancia del centro hacia cualquiera de los puntos del eje mayor.
3. La longitud del eje conjugado se define como dos veces la distancia del centro hacia cualquiera de los
puntos del vértice del eje menor.
Tipos
1. Hipérbola vertical: Si el centro de la hipérbola C(x0, y0) y el eje principal es paralelo a OY, los focos tienen de coordenadas F(x0, y0+ c) y F'(x0, y0 − c). Y la ecuación de la hipérbola será:
2. Hipérbola horizontal: Si el centro de la hipérbola es C(x0, y0) y el eje principal es paralelo a OX, los focos tienen de coordenadas F(x0+c, y0) y F'(x0− c, y0). Y la ecuación de la hipérbola será:
LEYES - PRINCIPIOS - NORMAS - EXCEPCIONES
Leyes
La Ley de Boyle, pv= C, es una relación hipérbola. Esto mismo se puede afirmar de la relación que existe entre dos cantidades. Cualesquiera que sean inversamente proporcionales.
Normas
Normas
Para identificar la ecuación canónica de una hipérbola:
- Ambas variables tienen que estar elevadas al cuadrado.
- El segundo miembro tiene que ser = 1.
- Los coheficientes de las variables tienen que ser distintos.
- Los coheficientes de las variables tienen que ser distintos.
- Los coheficientes con sus variables tienen que ser de diferente signo.
Teoremas
La ecuación de una hipérbola con centro en el punto C(h, k), y eje focal paralelo al eje X es de la forma:
(x - h)² / a² - (y - k)² / b² =1, sus focos son (h + c, k) y (h .- c, k) y sus vértices son (h – a, k) y (h + a, k).
Si el eje focal es paralelo al eje Y su ecuación es de la forma: (y - k)² / a² - (x - h)² / b² = 1, sus focos son (h , k + c) y (h, k - c) y sus vértices son (h - a, k ) y (h + a, k ).
Donde para cada parábola a es la longitud del semieje transverso, b la del semieje conjugado y c la distancia del centro a cada foco; a, b, c están ligadas por larelación c² = a² + b².. También la longitud de cada lado recto es 2b² / a y la excentricidad está dada por la relación e = c /a.
Ecuaciones
TEOREMAS, DEMOSTRACIONES Y ECUACIONES
Teoremas
La ecuación de una hipérbola con centro en el punto C(h, k), y eje focal paralelo al eje X es de la forma:
(x - h)² / a² - (y - k)² / b² =1, sus focos son (h + c, k) y (h .- c, k) y sus vértices son (h – a, k) y (h + a, k).
Si el eje focal es paralelo al eje Y su ecuación es de la forma: (y - k)² / a² - (x - h)² / b² = 1, sus focos son (h , k + c) y (h, k - c) y sus vértices son (h - a, k ) y (h + a, k ).
Donde para cada parábola a es la longitud del semieje transverso, b la del semieje conjugado y c la distancia del centro a cada foco; a, b, c están ligadas por la
Ecuaciones
Ecuación reducida en el origen de la hipérbola:
Ecuación de la hipérbola de eje horizontal:
- Si el centro de la hipérbola es C(x0, y0) y el eje principal es paralelo a OX, los focos tienen de coordenadas F(x0+c, y0) y F'(x0− c, y0). Y la ecuación de la hipérbola será:
Ecuación de la hipérbola de eje vertical:
- Si el centro de la hipérbola C(x0, y0) y el eje principal es paralelo a OY, los focos tienen de coordenadas F(x0, y0+c) y F'(x0, y0− c). Y la ecuación de la hipérbola será:
Ecuación general de la hipérbola:
PROCEDIMIENTOS
El procedimiento que se debe seguir para realizar un ejercicio de hipérbolas es el siguiente:
1. Cuando en el enunciado nos dan la ecuación general para transformarla en canónica y así poder encontrar las partes de la Hipérbola.Paso 1: Colocar el termino independiente del otro lado de la igualdad.
Paso 2: Agrupar las variables (x,y)
Paso 3: Sacar factor común dejando las variables al cuadrado con coheficiente 1
Paso 4: se completa el cuadrado.
Paso 5: Se suman los factores.
Paso 6: El termino independiente l pasamos dividiendo para igualar la ecuación a 1.
Paso 7: los términos que multiplican a los cuadrados los pasamos dividiendo y simplificamos.
Al tener la ecuación Canónica podemos deducir algunos puntos claves para la graficación de la hipérbola.
2. Cuando en el enunciado nos dan la ecuación canónica para convertirla en la ecuación general se deben realizar los siguientes pasos:
Paso 1: sacamos m.c.m para eliminar el denominador.
Paso 2: se resuelven los polinomios.
Paso 3: se resuelve la distributiva.
Paso 4: se iguala la ecuación a 0.
paso 5: se agrupan los términos semejantes.
- La ecuación resultante seria la ecuación general de la Hipérbola.
2. Cuando en el enunciado nos dan la ecuación canónica para convertirla en la ecuación general se deben realizar los siguientes pasos:
Paso 1: sacamos m.c.m para eliminar el denominador.
Paso 2: se resuelven los polinomios.
Paso 3: se resuelve la distributiva.
Paso 4: se iguala la ecuación a 0.
paso 5: se agrupan los términos semejantes.
- La ecuación resultante seria la ecuación general de la Hipérbola.
GRÁFICAS
Gráfica de la hipérbola horizontal.
EJERCICIOS ''TIPO''
Representa gráficamente
1.
ERRORES COMUNES
LINKS:
http://www.vitutor.com/geo/coni/hActividades.html
http://www.vitutor.com/geo/coni/h_5.html
http://www.vitutor.com/geo/coni/h_6.html
http://www.cidse.itcr.ac.cr/cursos-linea/SUPERIOR/t1-cónicas/4-Hipérbola/index.html
http://html.rincondelvago.com/elipse-e-hipérbola.html
Guia de cónicas de Alicia Díaz Escobar
1.
2.-
ERRORES COMUNES
* Resolucion de los polinomios.
* No identificar claramente el eje de la hipérbola.
* No identificar claramente el eje de la hipérbola.
* Escribir los signos contrarios.
* El cambio de signos de las coordenadas del centro C(h,k)
CONOCIMIENTOS PREVIOS
- Álgebra.
- Ecuaciones. (segundo grado)
- Aritmética (propiedades de los números reales).
LINKS:
http://www.vitutor.com/geo/coni/hActividades.html
http://www.vitutor.com/geo/coni/h_5.html
http://www.vitutor.com/geo/coni/h_6.html
http://www.cidse.itcr.ac.cr/cursos-linea/SUPERIOR/t1-cónicas/4-Hipérbola/index.html
http://html.rincondelvago.com/elipse-e-hipérbola.html
Guia de cónicas de Alicia Díaz Escobar

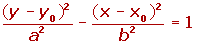
























Buena investigación excepto porque la ecuación general que colocaste está incompleta, le faltó decir que los coeficientes que acompañan a las variables al cuadrado deben ser de distinto signo. Por esta razón tienes un punto menos en la actividad.
ResponderEliminar